💬 La formalisation [...] doit être l’occasion d’introduire des représentations, sous forme de schémas bien adaptés, permettant la modélisation des problèmes proposés. Ces représentations sont systématiquement utilisées lors des résolutions de problèmes menées face à la classe, afin de servir de référence aux élèves. Elles ne sont bien sûr jamais rendues obligatoires (en particulier pour les élèves en réussite qui n’en ont pas besoin), mais doivent servir de point d’appui, lors des séances d’enseignement, avec les élèves rencontrant des difficultés lors de la résolution d’un problème.
L’objectif n’est pas d’établir un catalogue détaillé de typologies de problèmes pouvant exister, dont l’usage serait inopérant pour les élèves, mais au contraire de réunir les problèmes dans des catégories aussi larges que possible en faisant des analogies - Bulletin officiel spécial n°3 du 5 avril 2018
Une proposition basée sur quelques problèmes de référence
Propositions de schémas
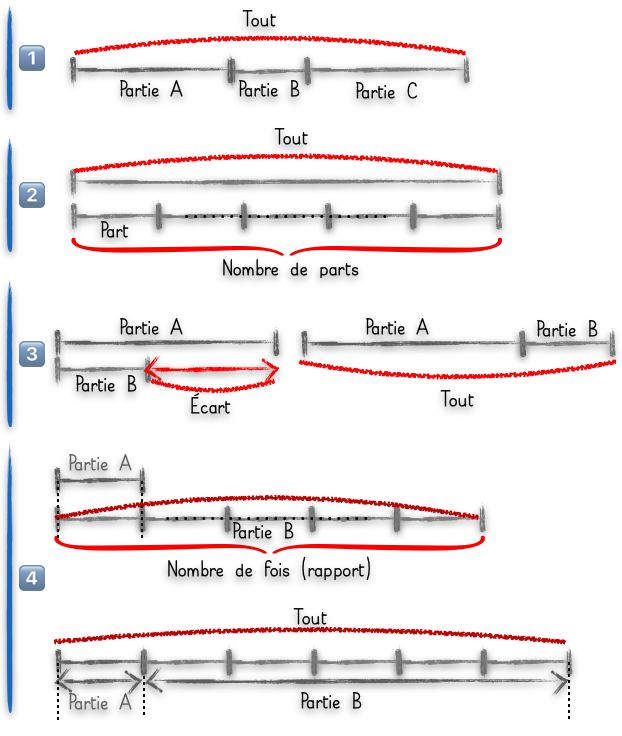
La catégorisation proposée ici regroupe les transformations et les compositions additives ou multiplicatives. C’est un choix particulier. Ce sont des problèmes qui se traitent de la même façon avec des schématisations similaires.
Les problèmes de gains et pertes (on compose les quantités ajoutées d’une part, et de l’autre les quantités déduites) se traitent ensuite avec un schéma de comparaison additive.
Les comparaisons additives et multiplicatives amènent à des problèmes plus complexes pour lesquels les recherches du ‘tout’, des partiess, ou des comparaisons (écart ou rapport) se traitent par des schémas parfois multiples.
